如果这篇博客帮助到你,可以请我喝一杯咖啡~
CC BY 4.0 (除特别声明或转载文章外)
预习报告
设计代码转换电路,输入为 4 位 8421 码,输出为 4 位循环码
逻辑真值表
| $B_3$ | $B_2$ | $B_1$ | $B_0$ | $G_3$ | $G_2$ | $G_1$ | $G_0$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
卡诺图化简
$G_3=B_3$显然。
| $B_3B_2\setminus B_1B_0$ | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 0 | 0 | 0 |
| 01 | 1 | 1 | 1 | 1 |
| 11 | 0 | 0 | 0 | 0 |
| 10 | 1 | 1 | 1 | 1 |
$G_2=B_3\overline{B_2}+\overline{B_3}B_2=B_3\oplus B_2$
| $B_3B_2\setminus B_1B_0$ | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 0 | 1 | 1 |
| 01 | 1 | 1 | 0 | 0 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 0 | 0 | 1 | 1 |
$G_1=B_2\overline{B_1}+\overline{B_2}B_1=B_2\oplus B_1$
| $B_3B_2\setminus B_1B_0$ | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 1 | 0 | 1 |
| 01 | 0 | 1 | 0 | 1 |
| 11 | 0 | 1 | 0 | 1 |
| 10 | 0 | 1 | 0 | 1 |
$G_0=B_1\overline{B_0}+\overline{B_1}B_0=B_1\oplus B_0$
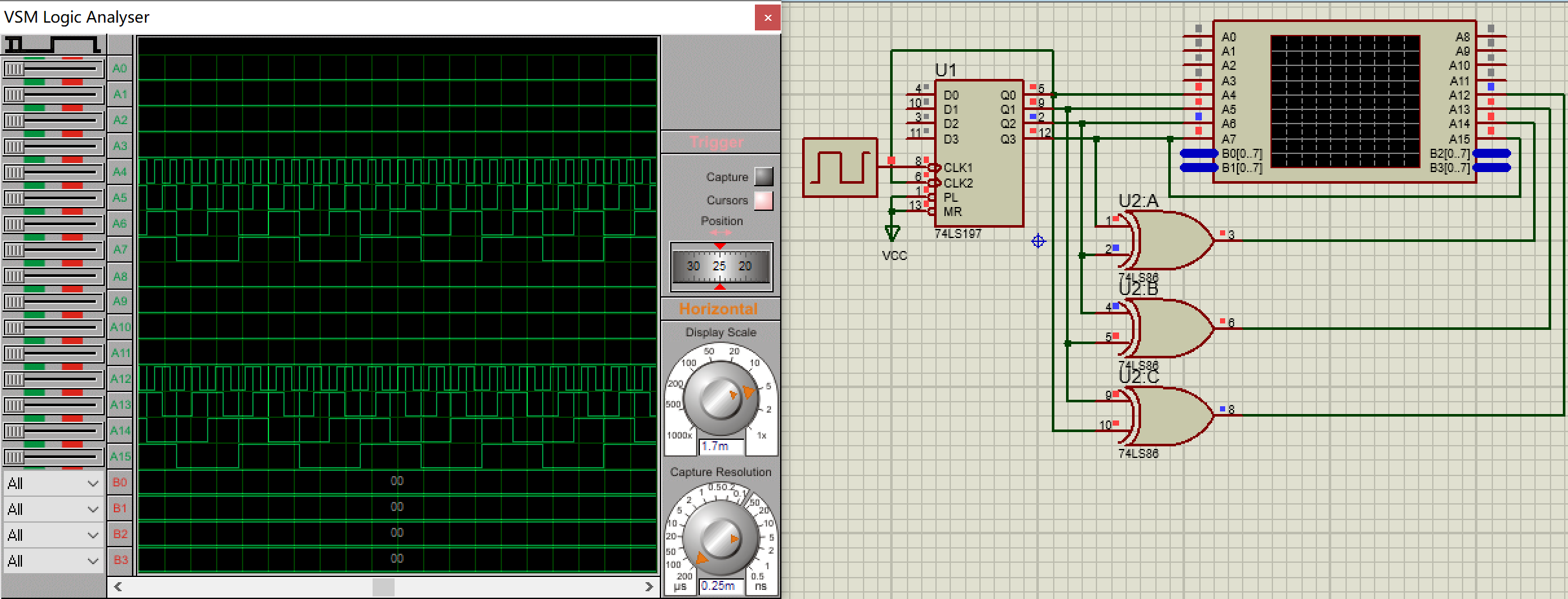
根据上述化简表达式,在proteus设计如下电路,并进行仿真
其中$A_4\ldots A_7$对应$B_0\ldots B_3$脚,$A_{12}\ldots A_{15}$对应输出$G_0\ldots G_3$脚;连续脉冲的频率为2kHz。 观察对应的波形可以发现,在$Q_0\ldots Q_3$输入电平对应0~9时,$G_0\ldots G_3$输出电平对应其循环码,符合上面的逻辑真值表。
实验报告
加分项:设计电路,完成虚拟数码管的8421码译码输出显示
思路
使用七块16线-1线选择器74150芯片,每块芯片控制原数码管上的一个段码(a~g)的输入端口。
真值表
| input\output | a | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 5 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 6 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| A | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| B | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| C | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| D | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| E | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| F | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
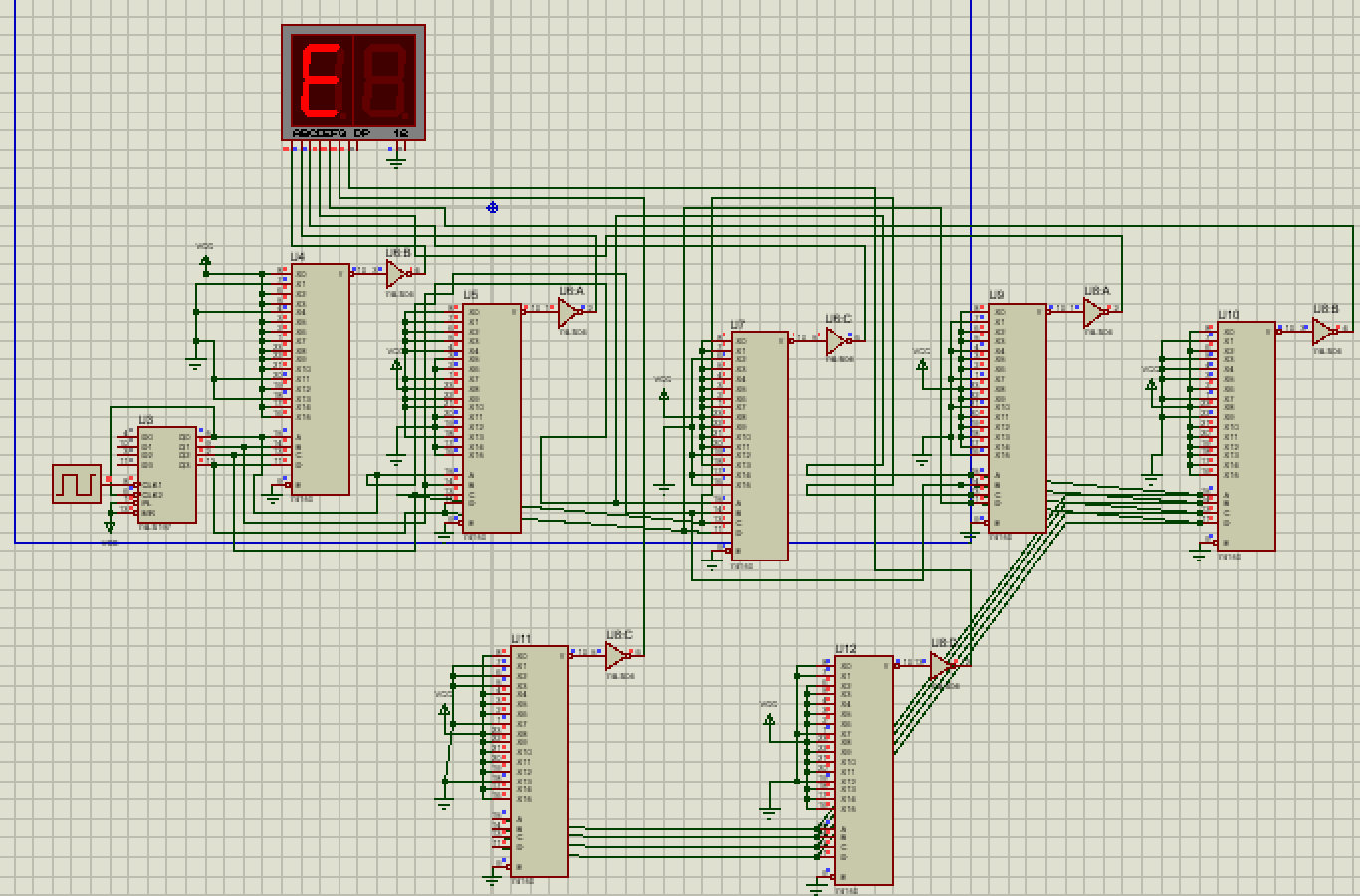
设计电路图
如图,使用74LS197构成16进制计数器作为代码转换电路的输入信号$Q_0\ldots Q_3$;连续脉冲的频率为1Hz 。
运行仿真

设计代码转换电路,输入为4位8421码,输出为4位循环码
实验仪器及器件
数字电路实验箱、万用表、示波器;器件:74LS86 *3、74LS197 *1
代码转换电路设计
具体设计和仿真已在预习报告中完成。
转换电路的效果检验及实验结果分析与讨论
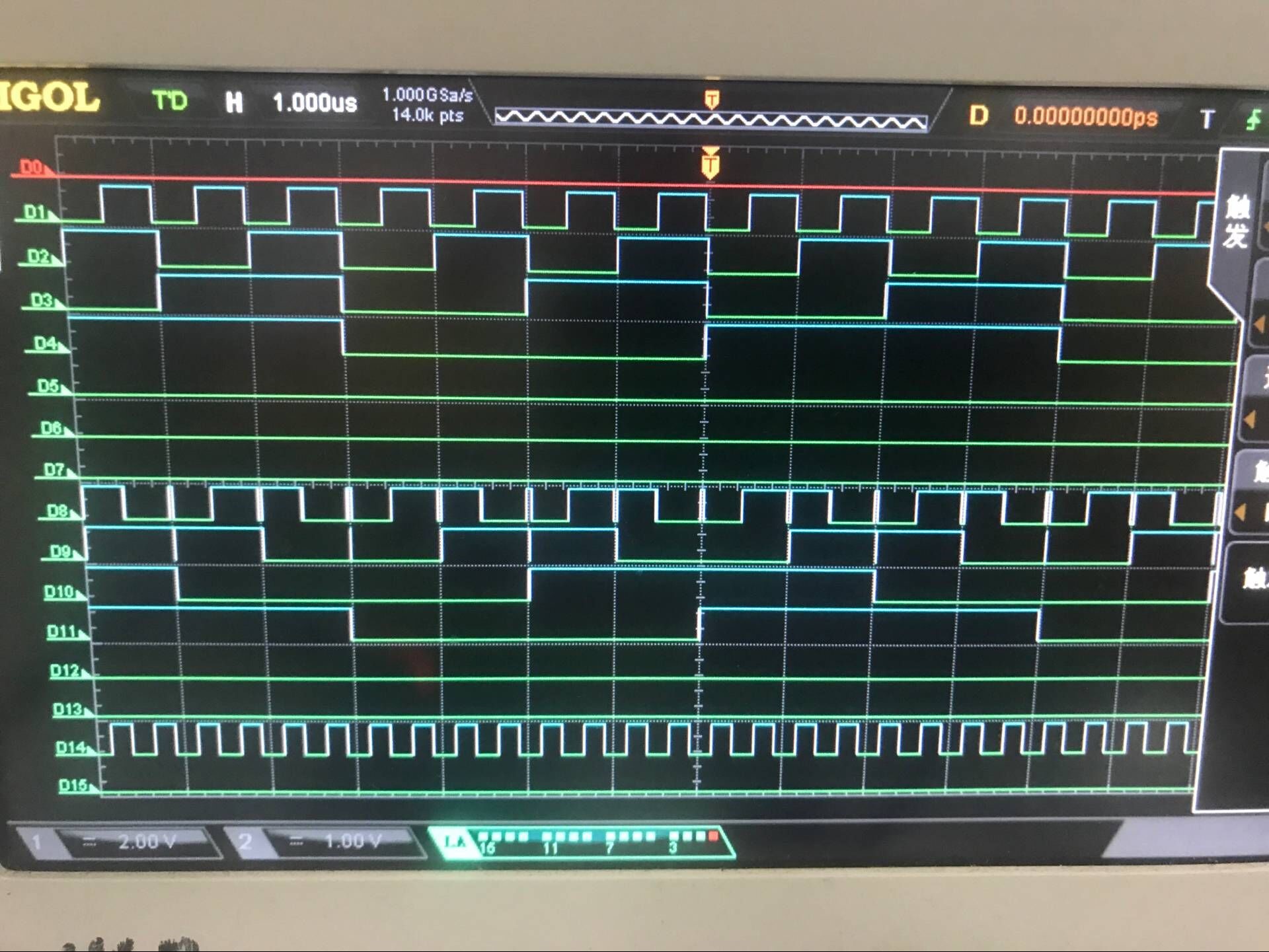
实验心得与体会
- 通过完成本实验,我基本了解组合逻辑电路的设计与分析过程。
- 预习过程中使用仿真软件对结果进行仿真期间让我对仿真软件有了更深的了解,加分项让我在找不到原有元件下如何利用其它元件组合来达到预期效果。
- 实验过程中对示波器的操作应更加熟练,要获得较为稳定的波形,还需要多次练习。